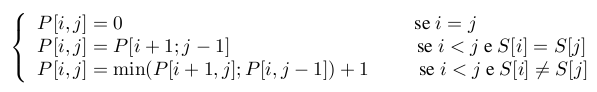Ricerca del minimo numero di caratteri da aggiungere a una stringa per renderla palindroma ( Compito del 28 Settembre 2011)
Il testo recita:
Una stringa e palindroma se non cambia leggendola da destra a sinistra e viceversa. Ad esempio anna e osso sono due palindromi.
Risolvere il seguente problema: data una stringa S = {a 1 , a2 , . . . , an } di n caratteri, calcolare il minimo numero di caratteri che occorre inserire per renderla un palindromo.
Suggerimento per la risoluzione:
Sia P [i, j] il numero di caratteri necessari per trasformare la stringa S[i, j] in una stringa palindroma. Il caso base consiste in una stringa di 1 (o meno) caratteri, cioè il caso in cui i = j.
In tal caso ovviamente non serve nessun carattere per rendere la stringa palindroma perch lo gi. Altrimenti se i caratteri S[i] ed S[j] sono uguali allora posso semplicemente risolvere il sottoproblema P [i + 1; j − 1]. Viceversa dovrò inserire almeno un carattere per rendere la stringa palindroma e calcolare il minimo tra i sottoproblemi P [i + 1; j] e P [i; j + 1], risolti ricorsivamente. La definizione ricorsiva di una soluzione ottima potrebbe essere così definita
La risoluzione del problema mediante l’utilizzo della programmazione dinamica prevede quindi la costruzione di una tabella di dimensione n × n.
Implementazione ricorsiva
int p(char s[], int da, int a){
if(da>=a)return 0;
if (s[a]==s[da])return p(s, da+1, a-1);
int r=p(s,da+1,a);
int l=p(s,da,a-1);
int x=r-l;
if(x>0)
return l+1;
else
return r+1;
}
int palindromizza(char stringa[]){
return p(stringa, 0, strlen(stringa)-1);
}
La fuzione viene implementata applicando semplicemente la formula di ricorsione
Implementazione Dinamica
int p_d(char s[], int da, int a, int r, int c, int v[ r ][ c ] )
{
if (da >= a)
{
return 0;
}
if (s[a] == s[da])
{
return v[da + 1][a - 1];
}
int destra = v[da + 1][a];
int sinistra = v[da][a - 1];
int delta = destra - sinistra;
if (delta > 0)
{
return sinistra + 1;
}
else
{
return destra + 1;
}
}
int p_iterativa(char stringa[])
{
int len=strlen(stringa);
int **v=malloc(sizeof(int)*len*len);
int i,j;
for(i=0;i<len;i++){
for(j=0;j<(len-i);j++){
int pal=p_d(stringa,j,i+j,len,len,v);
v[j*len+(i+j)]=pal;
}
}
len=v[len-1];
free(v);
return len;
}
L’implementazione dinamica viene creata modificando la funzione ricorsiva in modo che i valori già calcolati vengano letti da una matrice invece che ricalcolati. I valori per cui c>r sono necessariamente 0 (quelli sopra la diagonale principale) e non vanno calcolati.
L’unico modo di percorrere la matrice senza creare dipendenze da valori non ancora calcolati è per diagonali.
Esempi di matrici dei valori parziali
| [ 0 0 0 0 0 ] [ 0 0 0 0 1 ] [ 0 0 0 1 2 ] [ 0 0 1 0 1 ] [ 0 1 2 1 0 ]ABCBA -> 0 |
[ 0 0 0 0 0 ] [ 0 0 0 0 1 ] [ 0 0 0 0 1 ] [ 0 0 1 1 0 ] [ 0 1 0 1 1 ]pappa -> 1 |
[ 0 0 0 0 0 ] [ 0 0 0 0 1 ] [ 0 0 0 1 2 ] [ 0 0 1 2 3 ] [ 0 1 2 3 4 ]abcde -> 4 |