Dart, HTML5 e il frattale di Koch (1/2)

Qualche giorno fa ho cominciato a giocherellare con Dart, questo è il frutto della mia insonnia:

Dart, l’ennesimo tentativo di uccidere javascript.

Dart è un interessante progetto per creare un linguaggio cross-platform e cross-browser funzionante sia lato server che lato client che permetta di sviluppare applicazioni complesse.
L’obiettivo immediato è quindi il sostituire Javascript ( che è un linguaggio oggettivamente impossibile da debuggare ) e in futuro anche i linguaggi server side ( il primo che vorrei eliminare a questo punto è il php) permettendo di utilizzare un solo linguaggio per l’intera applicazione.
Dart dispone sia di una virtual machine ( ancora in alpha ) che un ricompilatore che permette di compilare in javascript in modo da rendere dart avviabile da qualunque browser moderno e ottenendo in futuro, quando la virtual machine si sarà diffusa, prestazioni superiori allo stesso javascript.
Dart è un linguaggio OOP che supporta la programmazione funzionale e può essere usato sia in maniera tipizzata che in maniera non tipizzata (tipizzazione opzionale la chiamano).Supporta l’ereditarietà singola e l’uso delle interfacce, e anche la reflection e la programmazione concorrente.
E’ un progetto molto interessante, non vedo l’ora che entri quantomeno in beta per cominciare a lavorarci seriamente.

La curva di Koch

Per il mio primo “toy program” in dart ho scelto di implementare una classe che disegni la curva di kock in una canvas HTML5.
Non era di geometria che volevo parlare nell’articolo ma descriverò anche matematicamente il modo in cui si può disegnare attraverso il calcolo vettoriale.
La curva di Koch è uno dei primi frattali conosciuti, la sua definizione è più vecchia della definizione formale dei frattali.
La curva si ottiene a partire da un segmento, il segmento viene diviso in 3 parti e nel sottosegmento centrale si ricava un triangolo equilatero, ottenendo quindi una figura formata da 4 segmenti.
La procedura si ripete per ogni segmento, prendo in prestito un immagine da Wikipedia

Animazione della costruzione del frattale di koch

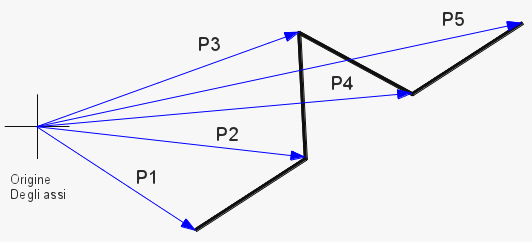
Descriverò la tecnica che ho utilizzato in modo matematico, la trasposizione in codice è abbastanza immediata. Per non perdere di generalità disegnerò una generica porzione del frattale che sia inclinata in modo non banale ( non orizzontale, non verticale e nemmeno a 45°) in modo da evitare che l’esempio ci porti a fare delle semplificazioni che non varrebbero nel caso generico della procedura.

Costruzione di un livello del frattale a partire da un segmento

1. Si divide il segmento (P1-P5) in 3 parti ottenendo il P2 e P4

Nel caso non ve lo ricordaste la divisione del segmento in un numero arbitrario di parti si ottiene estraendo il vettore che applicato al punto iniziale porta a quello finale, dividendone il modulo per la porzione che si vuole ottenere e applicandolo quindi al punto iniziale del segmento per ottenerne il punto finale.

2. Troviamo P3 applicando al punto medio del segmento ( che si trova come nel passo 1) un vettore lungo quanto l’altezza del triangolo (√(3/4) della lunghezza dei segmenti precedenti) e ruotato di 90° rispetto al vettore di partenza

La rotazione di un vettore si ottiene moltiplicandolo per la matrice di rotazione dell’angolo, nel caso di un angolo di 90° si ha: 

Ogni moltiplicazione per un vettore esprime una rotazione per una fase e una moltiplicazione per un modulo, una matrice di rotazione per un angolo α è la trasposizione in forma matriciale del vettore 1∠ α che equivale alla forma rettangolare cos(α)+ i sin(α) che corrisponde per definizione alla matrice

  List trovaramo(num x1, num y1, num x2, num y2){
    var p2=[x1+(x2-x1)/3,y1+(y2-y1)/3]; // un terzo del segmento
    var p3=[x1+(x2-x1)/2,y1+(y2-y1)/2];//il centro del segmento
    var p4=[x1+(x2-x1)*2/3,y1+(y2-y1)*2/3]; // due terzi del segmento
    var v=[(p2[0]-x1)*r3_4,(p2[1]-y1)*r3_4];
//un vettore allineato al segmento e lungo quanto l'altezza del triangolo
    var vr=[v[1],-v[0]]; //ruoto il vettore di 90 gradi
    p3=[p3[0]+vr[0],p3[1]+vr[1]];
// applico il vettore al punto medio del segmento per ottenere la punta del triangolo
    return [[x1,y1],p2,p3,p4,[x2,y2]];
  }