Contare le coppie adiacenti in una sequenza in tempo nLog(n) (Appello Settembre 2010)
il testo recita:
Sia data una sequenza di interi a1 , a2 , . . . , an . Diciamo che la sequenza contiene una coppia di numeri consecutivi se esistono due interi ai e aj tali che ai = aj + 1. Implementare un algoritmo per contare il numero di coppie consecutive contenute nella sequenza, che impieghi una complessità di tempo complessiva di n log n e una quantità di memoria aggiuntiva di O(n).
Implementazione attraverso un albero binario
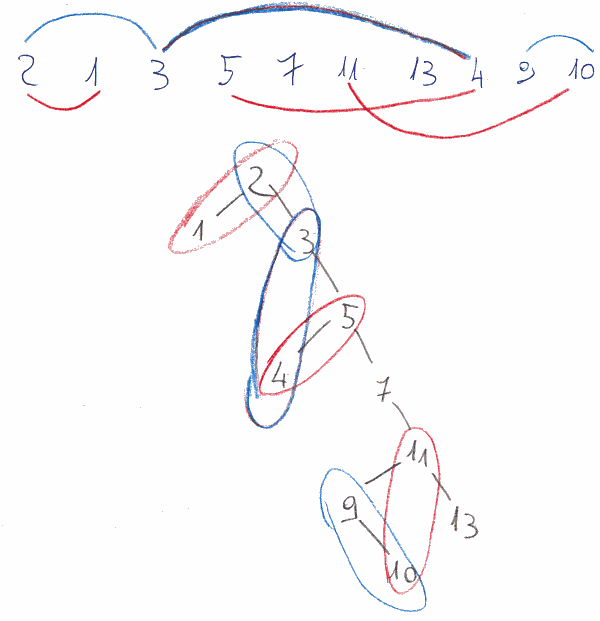
Il problema può essere risolto implementando una treesort e facendo in modo che in fase di inserimento si verifichi l’esistenza delle coppie adiacenti
#define N 10
#include "util.h"
#include "strutture.h"
#include <string.h> // NULL è definito qui
int piazza(nodo *base, nodo *nodo, int coppie){
int x=nodo->val-base->val;
if(x==1 || x==-1){//ho trovato una coppia
coppie++;
printf("coppia %d <-> %d (%d) \n",nodo->val,base->val, coppie);
}
if(x>0){//maggiore, vado a destra
if(base->r==NULL){//è vuoto, lo piazzo
base->r=nodo;
}else{//non è vuoto, richiamo
coppie=piazza(base->r, nodo, coppie);
}
}else{//è minore, vado a sinistra
if(base->l==NULL){//è vuoto, lo piazzo
base->l=nodo;
}else{//non è vuoto, richiamo
coppie=piazza(base->l, nodo, coppie);
}
}
return coppie;
}
void trovacoppie(int len, int v[len])
{
int coppie=0,n;
nodo *nodi=malloc(sizeof(nodo)*len);
for(n=0; n<len; n++)
{
nodi[n].val=v[n];
nodi[n].l=NULL;
nodi[n].r=NULL;
if(n>0)coppie=piazza(nodi, &nodi[n], coppie);
}
free(nodi);
printf("Un totale di %d coppie trovate\n", coppie);
}
Il contatore delle coppie viene passato a ogni chiamata ricorsiva e viene ritornato in output dalla funzione di ordinamento, in questo modo l’output finale conterrà il conto totale, questo approccio ha complessità O(n*log(n)) , non possono esistere soluzioni con un ordine di complessità minore inquanto non esistono ordinamenti più veloci essendo n*log(n) la dimensione dell’albero generato dalle decisioni necessarie per un ordinamento.
L’albero viene allocato dentro un vettore per facilitarne la deallocazione.